Medidas de tendencia central: ¿cómo usarlas para darle claridad a tus datos?

Si constantemente estás trabajando con datos, necesitas saber qué son las medidas de tendencia central. Pues se volverán tus mejores aliadas a la hora de hacer ese reporte final de métricas o de estado de proyectos que tanto necesitas para saber cómo se cumplieron los objetivos. 

Sabemos que existen ocasiones en las que debemos tratar con una gran cantidad de información, podemos tener un gran número de datos, números y variables y no siempre sabemos la mejor forma de resumirlos. ¡Aquí es donde entran las medidas de tendencia central a jugar! 

De acuerdo con Deloitte, “las mejores estrategias de datos generalmente se adaptan a las necesidades de la organización”, y es por eso que antes de lanzarte a calcular, lo primero que debes tener en cuenta son tus objetivos y qué información buscas en el análisis de los datos. 

En esta nota veremos todo sobre las medidas de tendencia central, qué son, cómo se miden y para qué podemos usarlas, además algunos ejemplos para que la siguiente vez que te sientas abrumado por muchos números y datos, sepas perfectamente cómo analizarlos.

¡Escoge tus tablas de datos y comencemos!

¿Qué son las medidas de tendencia central?

Las medidas de tendencia central son parámetros estadísticos que informan sobre el centro de distribución de la muestra o la población estadística. En otras palabras, es un número que se ubica hacia el centro de la distribución de los valores de una serie de observaciones o medidas, en la que se encuentra localizado el conjunto de los datos.

Si es la primera vez que escuchas el concepto de medidas de tendencia central, te recomendamos que comiences tu camino por el mundo de los datos para empresas en nuestro curso online de Fundamentos estadísticos para análisis de datos. Junto a Gabriel Mendoza, Strategy & Insights Lead en Google, aprenderás:

• Qué es la estadística de forma introductoria, así como la estadística descriptiva e inferencial.

• Qué son las medidas de tendencia central, de dispersión y cómo analizar variables aleatorias.

• Qué es un intervalo de confianza, qué es una regresión lineal, y cómo se desarrolla cada uno.

• Los principales gráficos para el análisis y visualización de datos, así como el uso de tablas de frecuencias. 

Fuente: Unsplash

¿Para qué sirven las medidas de tendencia central?

Las medidas de tendencia central tienen como objetivo definir en qué lugar se ubica el elemento o número promedio típico del grupo o serie de datos. Por ejemplo, si quiero saber cuál es la cantidad promedio de veces que dejar el carrito abandona en mi e-commerce en un mes, puedo definirlo usando la moda, que quiere decir la selección más frecuente. 

De la misma manera, las medidas de tendencia central nos sirven para comparar datos e interpretar los resultados que se obtienen de una serie de datos. Así, lo que podemos determinar es la diferencia de un valor con otro valor. Por ejemplo, la cantidad de veces que se dejó el carrito en determinado mes con respecto al otro.

Por otra parte, las medidas de tendencia central y los promedios nos ayudan a descartar cifras fuera del rango, es decir, anomalías, y de esta forma, trabajar con una serie de información limpia y ordenada. En este caso, podríamos determinar si tal o cual estrategia nos ayudó a disminuir los carritos abandonados. 

¿Acaso todas estas definiciones te hicieron dar cuenta que todavía no basas tus decisiones en datos tanto como deberías? ¡No te preocupes! Siempre hay tiempo de incorporar las medidas de tendencia central en tus estrategias, para eso Si los números y negocios son lo tuyo, te invitamos a suscribirte a nuestros cursos online de ciencias de datos, en donde encontrarás más de una solución a tus problemas. 

Fuente: Pexels

¿Cuáles son las medidas de tendencia central?

En esta sección veremos cuáles son las principales medidas de tendencia central, y cómo calcularlas e interpretarlas correctamente para que la toma de decisiones en tus estrategias administrativas o de marketing sean 100% fundamentadas. 

Según Economipedia, existen tres tipos principales de medidas de tendencia central:

• media
• mediana
• moda

1. Media

La media es la medida de tendencia central más utilizada. Es el valor promedio de un conjunto de datos numéricos. Se calcula sumando el total del conjunto de valores dividido entre el número total de valores, es decir, el tamaño de la muestra. Se expresa de la siguiente forma matemática:

¿Necesitas un poco más de guía para entender esta medida de tendencia central? Donde x es el valor de la observación o número i; N el total de observaciones o tamaño de la muestra. 

¿Cómo se calcula la media?

Supongamos que quiere determinar el promedio de la cantidad de ventas diarios en 8 días, y los datos que arroja tu tabla de excel son: 7,9,10,8,6,8,9,7

La media se calcula de la siguiente forma:

Suma de muestra = 7+9+10+8+6+8+9+7=64

Tamaño de la muestra (N) = 8

Media = 64/8 = 8

Como resultado, podemos decir que tu negocio tiene una media de 8 ventas diarias en 8 días.

2. Mediana

La siguiente medida de tendencia central es la mediana. Con mediana nos referimos al dato estadístico que parte exactamente a la mitad la misma cantidad de valores de un lado y del otro. 

Para calcular la mediana, lo que se debe hacer es “partir en dos” la muestra. Para hacer esto, es necesario agrupar los datos de menor valor a mayor valor, dejando la misma cantidad de valores de un lado que del otro.  Es diferente a la media ya que nos da la posición promedio del conjunto de datos.

La fórmula matemática de esta medida de tendencia central es la siguiente:

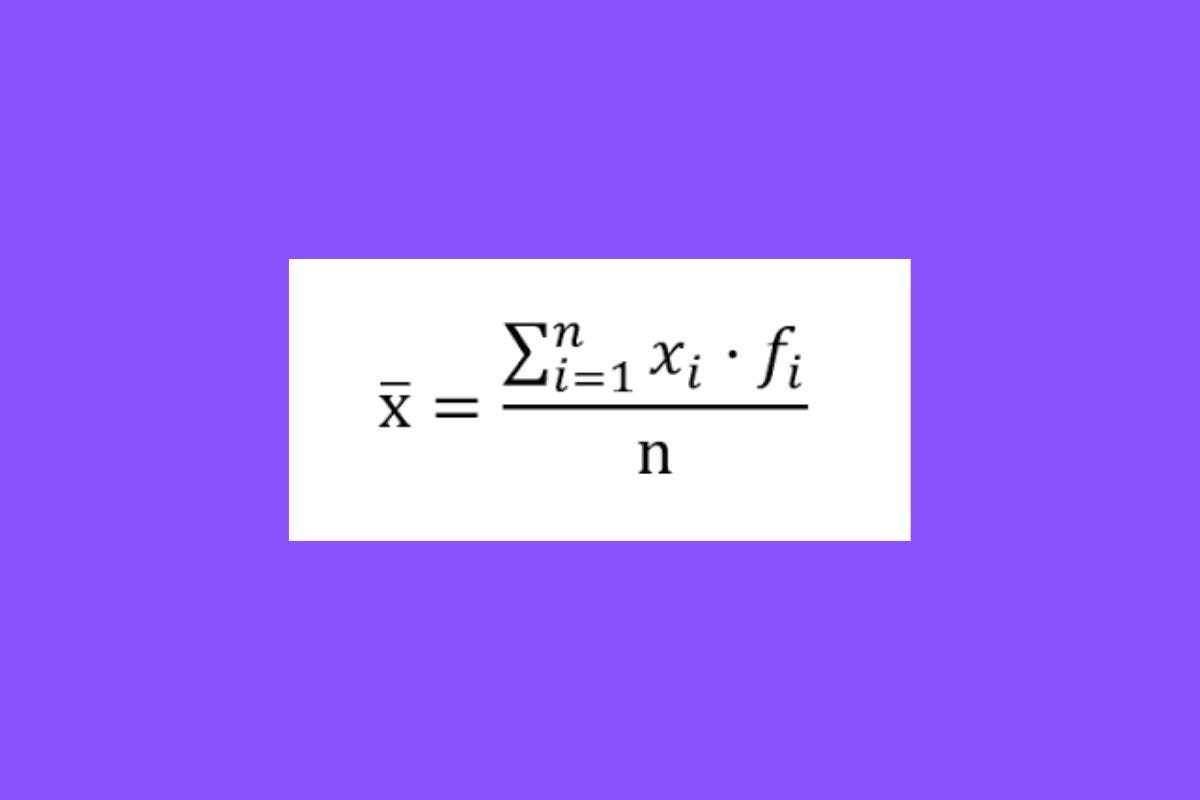
¿Cómo se calcula la mediana?

Supongamos que hay dos grupos distintos de clientes a los que quieres apuntar tu próxima estrategia, pero para eso quiere saber cuál es el punto medio de ventas entre ambos grupos, sin importar su distinción: 

1. El primer grupo consiste de 8 clientes responsables de las ventas que vimos arriba: 7,9,10,8,6,8,9,7
2. El segundo grupo consiste de 11 clientes y sus ventas son muy parecidas a las del primer grupo pero hay 3 alumnos más: 7,9,10,8,6,8,9,7,6,10,9

Lo importante aquí es que el primer grupo tiene un número par de clientes y el segundo tiene un número impar.

Por lo tanto, cuando el número de observaciones es par, como lo es en el primer grupo, la mediana se calcula de la siguiente manera: 

• Lo primero que se debe hacer es ordenar los datos de menor a mayor: 7,9,10,8,6,8,9,7 → 6,7,7,8,8,9,9,10
• Después ir eliminando los valores de ambos lados en dirección al centro: 6,7,7,8,8,9,9,10

En este caso, el punto medio son ambos valores de 8 por lo que la mediana es 8.

Cuando el número de observaciones es impar, se repite el mismo procedimiento. En el caso del segundo grupo, la mediana es:

7,9,10,8,6,8,9,7,6,10,9 → 6,6,7,7,8,8,9,9,910,10

6,6,7,7,8,8,9,9,9,10,10

El resultado es el valor central. En el segundo grupo con 11 clientes, el promedio o la mediana es 8. 

Como ya te imaginas, este es sólo un ejemplo de medida tendencia central y seguro en su caso tienes una pila de datos para comparar, por eso será conveniente que aprendas cómo usar la función mediana en Excel, gracias a este procesador de información los cálculos serán aún más sencillos 

Fuente: Pexels

3. Moda

Finalmente, llegamos a la moda. Esta medida de tendencia central es sencillamente el valor que más se repite en la muestra estadística o población. Si bien existe una fórmula matemática, lo más fácil de hacer es determinar cuál es el valor que más se repite.

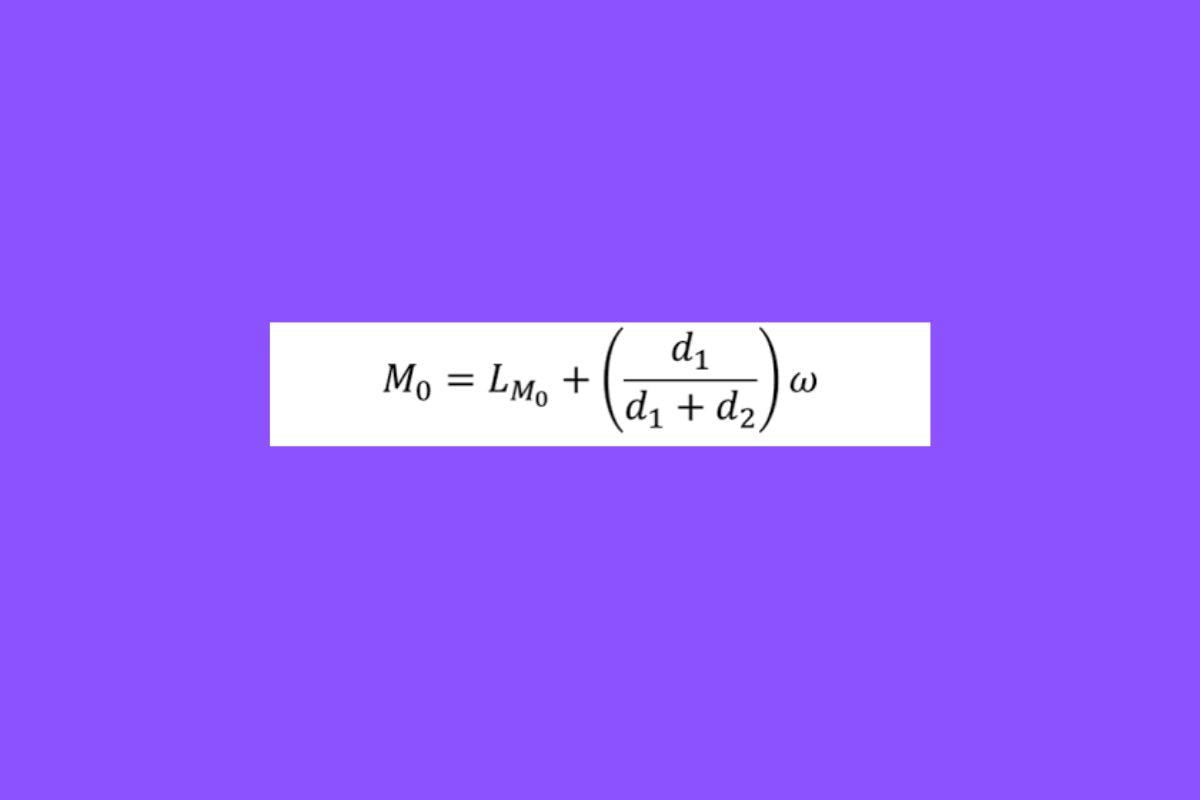
Imagina que estás a punto de sacar tu propia línea de textiles y necesitas saber las medidas promedio del público objetivo al que apuntas, para eso haces una encuesta y resulta que las estaturas de un grupo de 8 personas son:

1.75m, 1.78m, 1.64m, 1.82m, 1.75m, 1.68m, 1.75m, 1.88m

En este caso, la moda es 1.75m pues se repite en tres ocasiones, la mayor cantidad del grupo. 

A diferencia de la media y mediana, la moda también se puede calcular para observaciones no numéricas. Por ejemplo, se le preguntó al mismo grupo cuál es su comida favorita y responden lo siguiente:

Pizza, tacos, hamburguesas, pasta, pizza, tacos, pizza, sushi

En este caso, la moda es la pizza. 

Rango

Por último, existe el rango. Aunque bien éste no es una medida de tendencia central, nos sirve para ver la diferencia entre el menor y el mayor valor. Se calcula simplemente obteniendo la diferencia entre el mayor y menor valor.

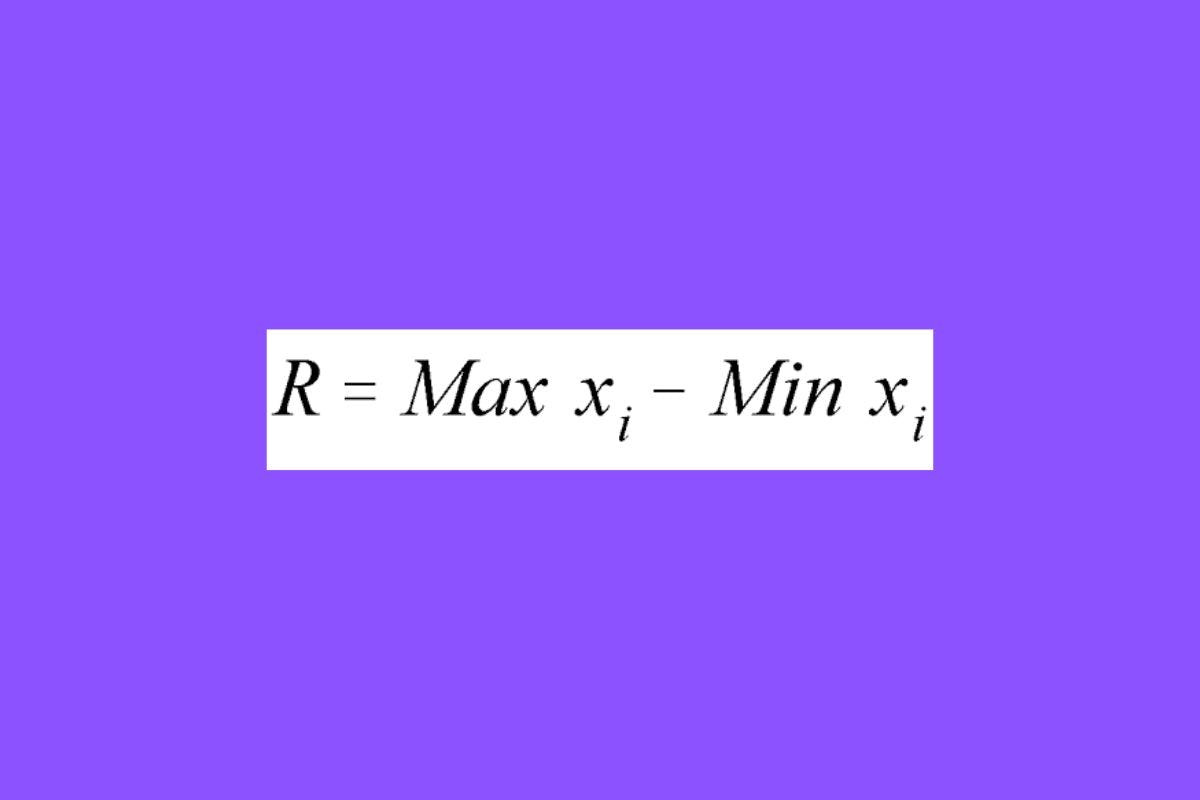
Para nuestro ejemplo de clientes del e-commerce, queremos conocer el rango de ventas:

7,9,10,8,6,8,9,7 → 10 - 6 = 4. El rango es 4.

Al igual que en el resto de los casos, estos son sólo ejemplos de medidas de tendencia central, pero en el caso de que tu volúmen de datos sea mucho mayor a un par de pizzas y tacos, puedes descargar totalmente gratis la plantilla de nómina en Excel y automatizar parte del cálculo en pocos clics.  

Fuente: Unsplash

Ya sabes todo sobre las medidas de tendencia central. Si quieres calcular un promedio muy preciso, la media es la opción. Pero no significa que la mediana y la moda no sirvan, también tienen sus usos. ¡Todo depende de los objetivos que necesites cumplir!

Recuerda que hacer estos cálculos es tan sólo el inicio, tú tienes todas las posibilidades de analizarlo como mejor veas. Pero el mundo del data analytics es mucho más grande de lo que piensas. Mientras tanto, continúa practicando con estas medidas de tendencia central.

¡Mucho éxito en los cálculos!