Antes de empezar a hablar de las fórmulas matemáticas y ecuaciones que cambiaron la historia, debes saber qué es una igualdad. Retrocedamos un poco a lo básico: comparar dos cosas que tienen el mismo valor, se denomina “igualdad”. A su vez, para que haya una igualdad, debe haber dos expresiones, una a cada lado del signo "igual" (=). Como en: “5 = 3 + 2”.
Ahora bien, ¿qué es una ecuación? Una ecuación es una igualdad en la que hay una “incógnita” o un “valor desconocido”. La “incógnita” se representa con una letra (“x”, “y”, “a”, “b”, “c”, etc.) y puede valer cualquier número. Te recordamos la primaria y la secundaria, ¿cierto?
En su libro “17 ecuaciones que cambiaron el mundo”, el científico Ian Stewart escribió sobre 17 ecuaciones y fórmulas matemáticas que cambiaron la historia, en donde analiza cada ecuación de forma práctica, acercándonos a cómo estas ecuaciones han afectado nuestras vidas y lo siguen haciendo. ¿Quieres saber cuáles son? ¡Vamos a ello!
 Imagen: twitter.com/proffeynman
Imagen: twitter.com/proffeynman
El teorema de Pitágoras
Hace más de dos mil años se produjo un descubrimiento sorprendente sobre los triángulos: cuando un triángulo tiene un ángulo recto (90°), y se hacen cuadrados en cada uno de los tres lados, el cuadrado más grande tiene exactamente la misma superficie que los otros dos cuadrados juntos.
Esta ecuación recibe el nombre de "teorema de Pitágoras", y puede escribirse en una breve ecuación matemática (a2 + b2 = c2).
 Imagen: mathisfun.com
Imagen: mathisfun.com
Como pudiste ver, “c” es el lado más largo del triángulo y “a” y “b” son los otros dos lados, llamados “catetos”. El lado más largo del triángulo se llama "hipotenusa", por lo que la definición formal del "teorema de Pitágoras" es:
“En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos”.
Hoy en día, esta es una de las fórmulas matemáticas que se utiliza con frecuencia desde la arquitectura, carpintería, pasando por la ingeniería hasta el diseño gráfico, y muchas otras disciplinas.
Por ejemplo, si vas a construir el tejado inclinado de una casa, sabiendo la altura del tejado y la longitud que debe cubrir, puedes utilizar el Teorema de Pitágoras para encontrar la longitud de la diagonal de la pendiente del tejado. Esta información te permite cortar las vigas del tamaño adecuado para sostener el tejado, o calcular el área que necesitarías tejar.
Todo el mundo recuerda el "teorema de Pitágoras", aunque no se sabe con certeza si fue él quien demostró por primera vez su validez. Algunos creen que incluso fueron los babilonios quienes la descubrieron, como también Euclides aportó pruebas sobre su utlización.
Logaritmos
En el segundo puesto de la lista de ecuaciones matemáticas que han cambiado el mundo, se encuentran los “logaritmos”.
Los logaritmos fueron descubiertos en 1614 por John Napier, un terrateniente escocés apasionado por las matemáticas. Fueron revolucionarias porque, gracias a las tablas logarítmicas, permitieron multiplicar grandes números de forma rápida y sencilla durante siglos hasta el desarrollo de las computadoras.
En su forma más sencilla, un logaritmo responde a la pregunta: “¿cuántas veces multiplicamos un número para obtener otro?” Por ejemplo:
“¿Cuántos 2s debemos multiplicar para obtener 8?” Respuesta: 2 × 2 × 2 = 8, así que tuvimos que multiplicar 3 de los 2s para obtener 8. De modo que el logaritmo es 3. Esta fórmula matemática puede parecerte ahora muy fácil pero, imagina en aquella época: ¡todo un descubrimiento!
Cálculo infinitesimal
Descrito a finales del siglo XVII por Isaac Newton y Gottfried Leibniz, aún se discute quién de los dos propuso primero la definición del cálculo infinitesimal, pero parece que los dos eruditos llegaron a ella de forma diferente e independiente.
Según Superproof, el cálculo infinitesimal es “una rama de las matemáticas que se ocupa del estudio de la variación y del movimiento. Permite observar y describir la realidad en términos dinámicos y se emplea en diversos campos tales como la física, la ingeniería, la economía o la estadística”.
Hay dos tipos de cálculo:
- El cálculo diferencial: determina la tasa de cambio de una cantidad, es decir, divide algo en trozos pequeños para averiguar cómo cambia.
- El cálculo integral: encuentra la cantidad cuando se conoce la tasa de cambio, o sea, une (integra) los trozos pequeños para averiguar cuánto hay.
Por ejemplo, las empresas de tarjetas de crédito utilizan el cálculo para otorgar el puntaje de crédito o fijar los pagos mínimos que deben realizarse en los extractos en el momento exacto en que se procesan. Claro está, teniendo en cuenta múltiples variables como los tipos de interés cambiantes y el saldo disponible fluctuante.
 Imagen: Pixabay
Imagen: Pixabay
Ley de la gravedad
Otra de las ecuaciones matemáticas fascinantes de la lista de Stewart es la “Ley de la gravitación universal” de Isaac Newton. ¿Por qué caemos al suelo cuando saltamos en vez de flotar en el espacio? ¿Por qué las cosas se caen cuando las lanzas o las dejas caer?
La respuesta es la gravedad: una fuerza invisible que atrae los objetos entre sí. La gravedad de la Tierra es lo que te mantiene en el suelo y lo que hace que las cosas se caigan.
La gravedad está a nuestro alrededor y actúa constantemente sobre un objeto para que vaya cada vez más rápido... en otras palabras, se acelera. Si ignoramos la resistencia del aire, su velocidad aumenta segundo tras segundo.
Casi todo lo que ocurre en nuestras vidas sucede sobre la superficie de la tierra, así que esta ecuación matemática se utiliza mucho.
La ley de Newton es una de las ecuaciones matemáticas más notables de la historia de la ciencia, porque explica, casi a la perfección, por qué los planetas se mueven como lo hacen, cómo funciona la gravedad en la tierra y en el sistema solar, o en cualquier parte del universo.
 Imagen: bbc.com
Imagen: bbc.com
Números complejos
Nuestra siguiente ecuación matemática es la “raíz cuadrada de -1”, de Leonhard Euler. Descubierta en 1750, dio lugar a los "números complejos".
Un número complejo es un número formado por una parte imaginaria y una parte real. Por lo tanto, se puede representar por la suma de un número real y un número imaginario (es decir, un múltiplo de la unidad imaginaria, denotado por la letra i).
Los números complejos se utilizan en todos los campos de las matemáticas, en muchos campos de la física, la mecánica cuántica, así como en la ingeniería y, especialmente, en la electrónica, telecomunicaciones e ingeniería eléctrica
Su importancia práctica, según Steward, es muy grande, ya que resulta esencial para entender tanto los sistemas eléctricos como una serie de algoritmos de procesamiento y análisis de datos.
A propósito, si quieres saber cómo calcular el retorno de inversión, con nuestra plantilla para calcular el ROI podrás conocer la rentabilidad de tu empresa con base en las finanzas de tu flujo de caja.
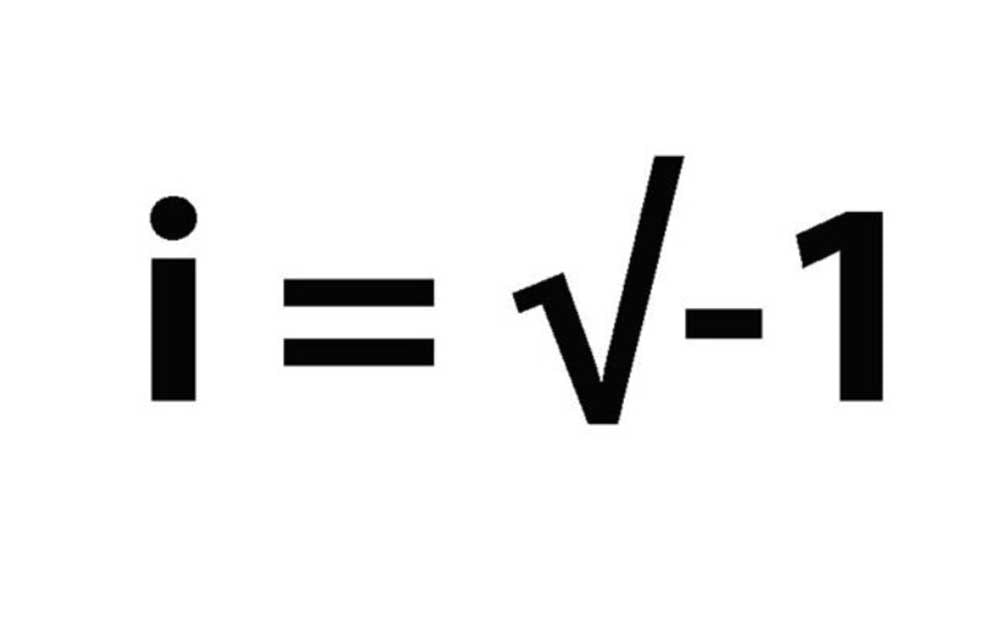 Imagen: bbc.com
Imagen: bbc.com
Fórmula de Euler para los poliedros
Un poliedro es un sólido tridimensional que está delimitado por polígonos (figura geométrica bidimensional) llamados caras. De hecho, la palabra poliedro viene del griego clásico πολύεδρον (polyedron), de la raíz πολύς (polys), "muchas" y de ἕδρα (hedra), “base”, “asiento”, “cara”.
Para cualquier poliedro que no se intersecte a sí mismo, el…
- Número de caras
- más el Número de Vértices (puntos de esquina)
- menos el número de aristas
- siempre es igual a 2
Esto se puede escribir: C + V - A = 2
En geometría de los sólidos, la fórmula matemática de Euler para los poliedros relaciona los números C (caras), V (vértices) y A (aristas) de un poliedro simple. La suma de las caras y las vértices menos las aristas es siempre 2.
Por ejemplo, un cubo tiene 6 caras, 8 vértices y 12 aristas, por lo que 6 + 8 - 12 = 2
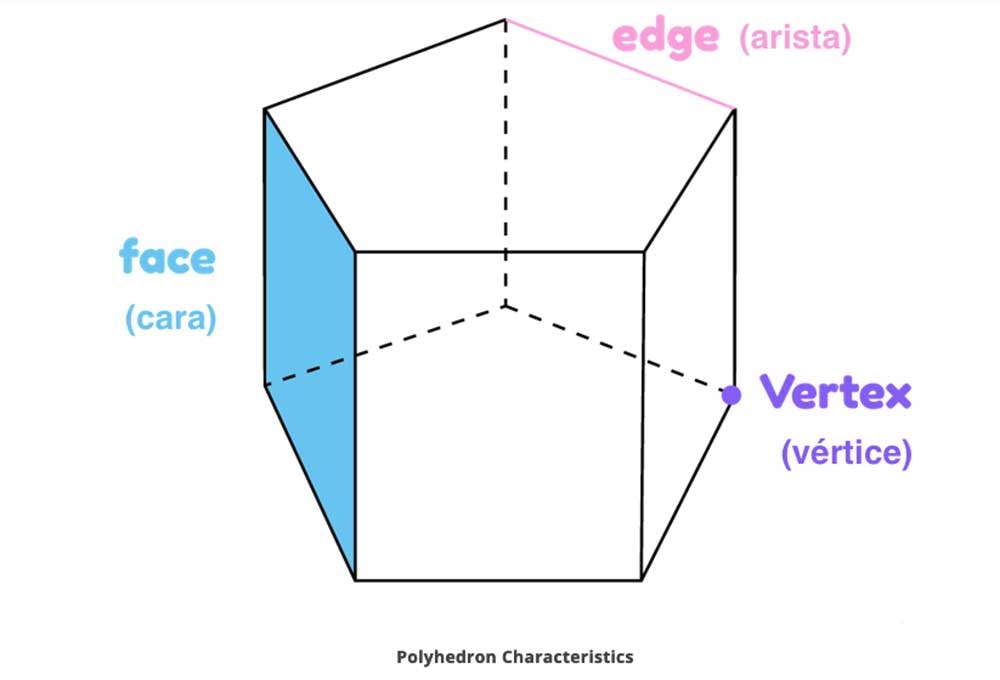 Imagen: calcworkshop.com
Imagen: calcworkshop.com
La distribución normal (o gaussiana)
En el séptimo lugar de las fórmulas matemáticas que han cambiado la historia se encuentra la “distribución normal”. La ecuación matemática fue formulada en 1810 por Carl Friedrich Gauss, conocido como el “príncipe de las matemáticas” y es uno de los pilares de la estadística.
Esta ecuación matemática se caracteriza por el gráfico de la “curva de campana”, es omnipresente en la estadística, y se emplea para modelar propiedades. De hecho, muchas cosas siguen de cerca una distribución normal:
- La altura de las personas
- El tamaño de las cosas producidas por las máquinas
- Los errores en las mediciones
- La presión sanguínea
- Marcas en un examen
La “distribución gaussiana” se utiliza para describir el comportamiento de grandes grupos de procesos independientes, ya que los datos pueden estar "distribuidos" (repartidos) de maneras diferentes, más a la izquierda, más a la derecha, o bien puede estar todo revuelto.
Pero hay muchos casos en los que los datos tienden a estar alrededor de un valor central sin sesgo a la izquierda o a la derecha, acercándose a lo que se le conoce como "Distribución Normal".
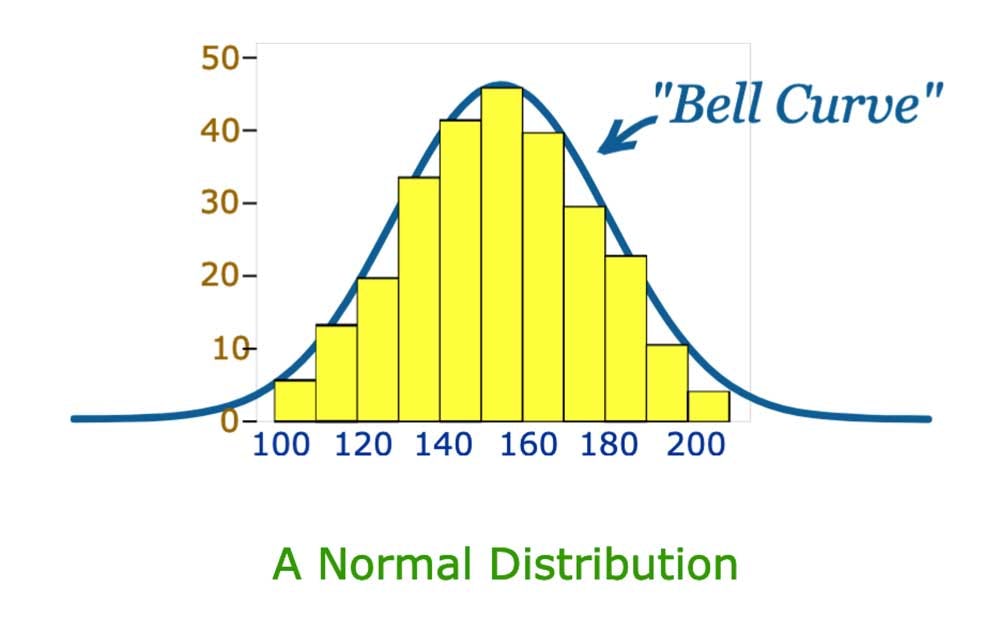 Imagen: mathsisfun.com
Imagen: mathsisfun.com
Ecuación de onda o ecuación de d'Alembert
Una forma alternativa de la segunda ley del movimiento de Newton, el “Principio de d'Alembert” fue enunciado por el polímata francés del siglo XVIII Jean le Rond d'Alembert.
Esta ecuación matemática diferencial describe el comportamiento de las ondas. Las ondas transfieren energía, no materia. La materia puede rebotar hacia arriba y hacia abajo (transversal), o hacia adelante y hacia atrás (longitudinal), pero en general no va a ninguna parte.
Por ejemplo, la cuerda de una guitarra que vibra, las ondas de un estanque tras el lanzamiento de una piedra o la luz que sale de una bombilla incandescente. Otra de las fascinantes fórmulas matemáticas que han cambiado la historia.
 Imagen: Pixabay
Imagen: Pixabay
Transformada de Fourier
Desarrollada en 1822 por el matemático francés Jean Baptiste Joseph Fourier, la “Transformada de Fourier” es otra de las fórmulas matemáticas de la lista de Stewart que cambiaron la historia.
Esta ecuación matemática tiene diversos usos que van desde la medicina, las telecomunicaciones, la ingeniería acústica, los circuitos eléctricos, pasando por el diseño de puentes frente a resonancias hasta la compresión de pistas de audio, y demás funcionalidades.
 Imagen: Pixabay
Imagen: Pixabay
Ecuaciones de Navier-Stokes
En 1821, el ingeniero francés Claude-Louis Navier introdujo el elemento de viscosidad (fricción) para el problema de los fluidos viscosos. Y a mediados del siglo XIX, el físico y matemático británico Sir George Gabriel Stokes mejoró esta ecuación matemática diferencial para estudiar los fluidos.
Las ecuaciones matemáticas de Navier-Stokes describen el comportamiento de todo lo que fluye: el agua que se mueve por una tubería, la leche que se mezcla con el café, el flujo de aire sobre el ala de un avión o el humo que sale de un cigarrillo.
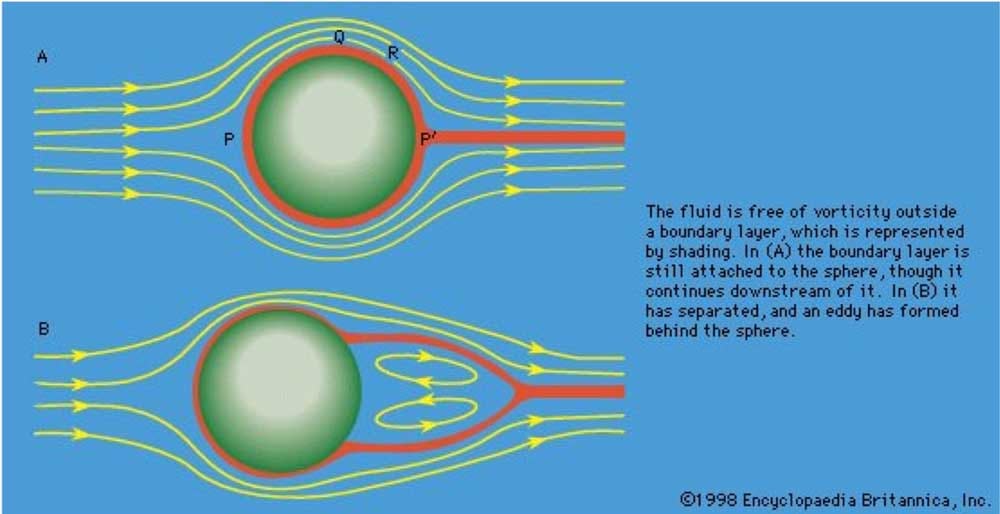 Imagen: britannica.com
Imagen: britannica.com
Ecuaciones de Maxwell
Las ecuaciones matemáticas de Maxwell son para el electromagnetismo lo que las leyes del movimiento de Newton son para la mecánica.
James Clerk Maxwell tradujo a ecuaciones los trabajos de Michael Faraday sobre la relación entre la electricidad y el magnetismo. Es decir, mediante complejas fórmulas matemáticas es posible describir la relación entre los campos eléctricos y magnéticos.
Al principio, se trataba de 20 ecuaciones, pero finalmente fueron unificadas en 4, gracias al trabajo de James Clerk Maxwell en 1863.
 Imagen: Pixabay magnet
Imagen: Pixabay magnet
Segunda Ley de la Termodinámica
La formulación más común del segundo principio de la termodinámica es la de Clausius: "Es imposible realizar una transformación cuyo único resultado sea la transferencia de calor de un cuerpo más frío a otro más caliente sin la contribución de un trabajo externo".
Este principio establece la irreversibilidad de los fenómenos físicos, especialmente durante el intercambio de calor, y que nunca será espontáneo. También se le conoce como “entropía”, que es una medida del desorden de un sistema físico aislado.
La mayor parte de los procesos físicos son reversibles, es decir, que se pueden aplicar las ecuaciones matemáticas al revés sin que se produzcan problemas. Sin embargo, la segunda ley sólo funciona en esta dirección.
De hecho, las máquinas térmicas son sistemas que transforman calor en trabajo. En ellas, se reflejan claramente las restricciones señaladas anteriormente: la máquina de vapor, el motor de un vehículo, e incluso un refrigerador (una máquina térmica funcionando en sentido inverso).
Hasta aquí, nuestro artículo sobre las fórmulas matemáticas y ecuaciones que cambiaron la historia. Para ti, ¿cuál ha sido la más importante? Quizá ya estés utilizando algunas de estas fórmulas matemáticas y ecuaciones en tus negocios sin haberlo sabido.
Tal vez quieras animarte ahora a inscribirte en el curso de Análisis y visualización de data con el profesor Juan Escobar, en donde aprenderás la importancia del data storytelling y la visualización de datos para tomar decisiones informadas.
Esperamos que este contenido haya sido útil e informativo. Esta entrada de blog se basó en la publicación del libro de Ian Stewart “17 Equations That Changed the World” (17 ecuaciones que cambiaron el mundo) y en el artículo de Busines Insider sobre su libro. Recuerda echar un vistazo a los cursos de Emprendimiento y Negocios que tenemos para ti. ¡Hasta la próxima!