Conocer el teorema de Pitágoras es muy útil para quienes tienen interés en aprender matemáticas y geometría. Sin embargo, algunas veces puede ser difícil de entender, sobre todo porque la mayoría de las personas complica las cosas y no va a lo concreto.

Por eso, en este artículo queremos explicarte qué es el teorema de Pitágoras, enseñarte cuál es su fórmula, ayudarte a descubrir cómo calcular la hipotenusa y el valor de los catetos de un triángulo rectángulo con un par de ejemplos muy sencillos.

Cuando termines de leer este blog post no solo sabrás escribir la fórmula del teorema de Pitágoras algebraicamente, sino que entenderás el concepto detrás de ella y serás capaz de usarla para resolver algunos ejercicios simples. Para lograrlo solo debes tener un conocimiento mínimo sobre las partes de un triángulo y saber resolver ecuaciones simples.

¿Qué es el teorema de Pitágoras?

El teorema de Pitágoras es una de las contribuciones más importantes a la matemática y la geometría en toda la historia, en él se establece que en los triángulos rectángulos, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Se trata de una noción básica de matemática y geometría que regularmente se estudia en la primaria.

Euclides, un matemático griego, fue quien algunos siglos después le daría la autoría del teorema a Pitágoras, un filósofo y matemático griego que vivió en el siglo VI a.C. Sin embargo, algunos autores han señalado que el teorema de Pitágoras fue descubierto mucho tiempo antes en Babilonia.

En palabras de los expertos, el teorema de Pitágoras es una de las fórmulas matemáticas que cambiaron el mundo, principalmente, porque le permitió a la humanidad conocer nuevos aspectos de la realidad.

Fuente: Unsplash

¿Cuál es la fórmula del teorema de Pitágoras?

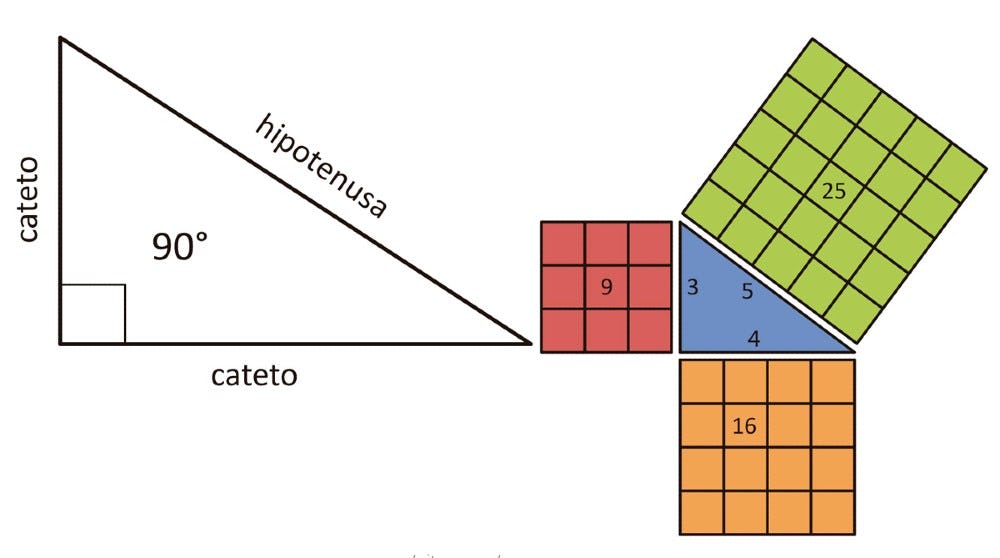
La fórmula del teorema de Pitágoras es: a²+b²= c². En esta fórmula a²+b² representan la suma de los catetos, mientras que c² representa la hipotenusa de un triángulo rectángulo.

A pesar de que la fórmula del teorema de Pitágoras se escribe en notación algebraica, es muy importante que sepas que no hay evidencia que muestre que la fórmula se escribía en términos algebraicos originalmente. De hecho, en el momento en el que se desarrolló el teorema de Pitágoras, no manejaban el concepto de álgebra.

El teorema de Pitágoras se suele utilizar en la enseñanza de matemáticas, y en la mayoría de los ejercicios que se pone en práctica, es necesario calcular la hipotenusa o el valor de alguno de los catetos. Sabiendo cómo se escribe el teorema de Pitágoras algebraicamente, lo único que tienes que hacer es reemplazar los datos y hacer una pequeña ecuación.

Fuente: ABC

Aplicaciones del teorema de Pitágoras

Para poner en práctica la fórmula del teorema de Pitágoras, lo mejor que podemos hacer es calcular el valor de la hipotenusa y de los catetos de algunos triángulos rectángulos. Estos ejemplos te ayudarán a entender mejor el concepto, y seguramente te servirán de referencia para hacer tus propios ejercicios.

Calcular la hipotenusa de un triángulo rectángulo

Para calcular la hipotenusa, utilizando el teorema de Pitágoras, es necesario conocer el valor de los catetos. Digamos que tenemos un triángulo rectángulo cuyos catetos tienen un valor de 3 y 4 cm respectivamente, en ese caso, la fórmula del teorema de Pitágoras quedaría de la siguiente manera:

c²= 3²+4² o c= √(3²+4²)

De cualquiera de las dos maneras se puede escribir la fórmula del teorema de Pitágoras para calcular el valor de la hipotenusa. Veamos cuál es el resultado usando la segunda notación algebraica.

1. Se empieza por resolver la operación que está en el paréntesis

1.1. c= √(9+16)

1.2. c= √(25)

2. Se calcula la raíz cuadrada

2.1. c= 25

Calcular el valor de un cateto en un triángulo rectángulo

Ahora vamos a calcular el valor de uno de los catetos utilizando el teorema de Pitágoras. Al igual que la operación anterior, es necesario conocer el valor de al menos dos datos, es decir, el valor de la hipotenusa y de uno de los catetos.

Por ejemplo, digamos que la hipotenusa tiene un valor de 10 cm y uno de los catetos tiene un valor de 8 cm. En este caso, la fórmula del teorema de Pitágoras quedaría de la siguiente manera:

a²= c²-b² o a= √(b²-c²)

Veamos cuál es el resultado de esta operación utilizando la primera notación algebraica.

1. Se reemplazan los valores de la fórmula

a²= 10²-8²

2. Se eleva cada número a su potencia

a²= 100-64

3. Se hace la resta

a²= 36

4. Se despeja la ecuación

a= √36

5. Se calcula la raíz

a= 6

Aplicando el teorema de Pitágoras, el resultado de esta operación nos indica que el valor del cateto a es de 6 cm. Este ejemplo te sirve para calcular cualquiera de los catetos de un triángulo rectángulo, solo debes asegurarte de escribir bien la fórmula del teorema de Pitágoras y seguir todos los pasos tal como te lo mostramos.

Si las matemáticas son lo tuyo y se te hizo muy sencillo aplicar el teorema de Pitágoras, te recomendamos explorar nuestro catálogo de cursos de administración de empresas. Es muy probable que con ellos le puedas sacar provecho a tus habilidades con los números.

Fuente: Unsplash

Ejemplos del teorema de Pitágoras en la vida cotidiana

Las personas suelen perder el interés en las matemáticas porque no entienden cómo los conceptos que aprenden en clase se pueden aplicar a la vida real. Por ejemplo, la mayoría de las personas se aprende la fórmula del teorema de Pitágoras, es capaz de calcular la hipotenusa, los catetos y todo lo que haga falta, pero no sabe representar eso en un ejercicio que vaya más allá del papel.

Pero las matemáticas están relacionadas con todo, de hecho, el teorema de Pitágoras se diseñó con el propósito de entender ciertos aspectos de la realidad. En ningún momento alguien pensó en crear un concepto abstracto para mantener a las personas haciendo cuentas.

Así que en esta parte te queremos comentar cuáles son algunas de las aplicaciones del teorema de Pitágoras en el la vida cotidiana, con el propósito de que entiendas cuál es su valor y por qué razón se sigue enseñando. ¡Todas las operaciones básicas de matemáticas tienen un propósito y una utilidad!

Arquitectura y construcción

El teorema de Pitágoras es utilizado comúnmente en la arquitectura y en la construcción, porque permite, por ejemplo, conocer cuál es la longitud de una diagonal que conecta dos líneas.

Si pensamos en ejercicios para aplicar el teorema de Pitágoras en la arquitectura y la construcción, podríamos decirte que calcules la inclinación de un techo, tomando como referencia la altura y la longitud del lugar en el que se va a instalar.

Como puedes ver, es un ejemplo sencillo en el que el teorema de Pitágoras resulta de gran utilidad.

Fuente: Unsplash

Navegación

Con el teorema de Pitágoras también se pueden hacer cálculos útiles al momento de navegar, y no solo hablamos de barcos. Por ejemplo, un piloto de avión puede hacer los cálculos para saber cuándo empezar el aterrizaje usando la fórmula del teorema de Pitágoras.

Lo único que necesita es conocer su altitud y la distancia que existe desde el punto en el que se encuentra hasta el aeropuerto en el que pretende aterrizar.

Fuente: Unsplash

El legado de Pitágoras se ha mantenido vivo hasta la actualidad, sus descubrimientos lo han convertido en uno de los nombres más conocidos en el mundo de las matemáticas y la geometría. El teorema que lleva su nombre aportó un conocimiento valioso para el desarrollo de la ciencia y la tecnología en sus momento, tanto que forma parte de la historia.

Ahora que conoces qué es el teorema de Pitágoras y que viste algunos ejercicios para tener una referencia de cómo funciona, solo te queda practicar y mantener vivo el conocimiento. 

Por cierto, si disfrutaste de este artículo, puedes haber descubierto una nueva pasión, así que vale la pena que revises algunas carreras con matemáticas que puedes elegir para estudiar y desarrollarte profesionalmente.

¡Hasta pronto!